Answer:
a) The probability that at least 5 ties are too tight is P=0.0432.
b) The probability that at most 12 ties are too tight is P=1.
Explanation:
In this problem, we could represent the proabilities of this events with the Binomial distirbution, with parameter p=0.1 and sample size n=20.
a) We can express the probability that at least 5 ties are too tight as:
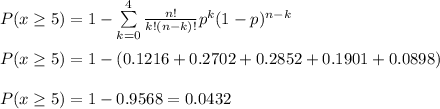
The probability that at least 5 ties are too tight is P=0.0432.
a) We can express the probability that at most 12 ties are too tight as:
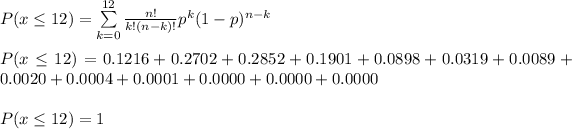
The probability that at most 12 ties are too tight is P=1.