Answer:
t1= 1.1475 sec
t2=9.48 sec
Explanation:
This question asking for the time when an object reach a specific height. I will explain what the formula stand for to make this easier.
h= height = 174feet
v0= initial velocity = 170 feet/s
t= time
h0= initial height= ground level = 0
The question have predetermined formula for the height, so we should use it instead of formula that involve gravity value.
h= -16
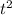 +v0t + h0t
+v0t + h0t
174 feet = -16
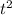 + 170 feet/s x t + 0 x t
+ 170 feet/s x t + 0 x t
-16
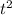 + 170 feet/s x t - 174 feet = 0
+ 170 feet/s x t - 174 feet = 0
8
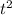 - 85 feet/s x t + 87 feet = 0
- 85 feet/s x t + 87 feet = 0
This equation will be hard to solve since its value in fraction, so lets use the quadratic formula
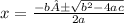
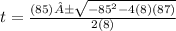
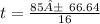
t1=
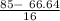
t1= 1.1475
t2=
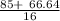
t2=9.48