Question

6. Use the diagram to answer the following.

(4x - 30)
(y)
6(z + 8)
3(x - 1)º

a. Find the values of x, y, and z that makes
p || 9 and 9 || r. Explain your reasoning.
b. Is p || r? Explain your reasoning.
90
Geometry
Resources by Chapter​

Answer 1

a.
`x=27,y=13,z=9`

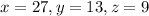
b. Yes, p || r.

Explanation:

a.

From the figure,

Since, p || q,

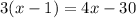`3(x-1)=4x-30` (∵ Alternate exterior angles are equal for parallel lines)

This gives,

`3x-3=4x-30\\4x-3x=-3+30\\x=27`

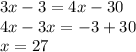
Now, q || r

∴
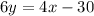`6y=4x-30` (∵ Corresponding angles are equal for parallel lines)

This gives,

`6y=4(27)-30\\6y=78\\y=13`

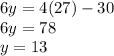
Now, since r is a straight line,
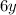`6y` and
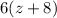`6(z+8)` are supplementary angles.

`6y+6(z+8)=180\\6(13)+6z+48=180\\78+48+6z=180\\6z=180-(78+48)\\6z=54\\z=(54)/(6)=9`

Therefore,
`x=27,y=13,z=9`.

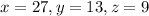b.

`3(x-1)=3(27-1)=3(26)=78\\6y=6* 13=78`

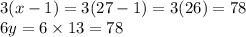
Since, alternate exterior angles
`3(x-1)` and
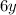`6y` are equal, the lines p and r are parallel because, alternate exterior angles are equal only if two lines are parallel.