Question

According to the U.S. Bureau of Labor Statistics, 75% of the women 25 through 49 years of age participate in the labor force. Suppose 78% of the women in that age group are married. Suppose also that 61% of women 25 through 49 years of age are married and are participating in the labor force. (Round your answers to 2 decimal places.)a. What is the probability that a randomly selected woman in that age group is married or is participating in the labor force?p = __________.b. What is the probability that a randomly selected woman in that age group is married or is participating in the labor force but not both?p = __________.c. What is the probability that a randomly selected woman in that age group is neither married nor participating in the labor force?p = __________.

Answer 1

a) There is a 92% probability that a randomly selected woman in that age group is married or is participating in the labor force.

b) There is a 31% probability that a randomly selected woman in that age group is married or is participating in the labor force but not both.

c) This means that there is an 8% probability that a randomly selected woman in that age group is neither married nor participating in the labor force.

Explanation:

We can solve this problem building the Venn's diagram of these probabilities.

I am going to say that

The set A are those women who participate in the work force.

The set B are those women who are married.

We have that:

`A = a + (A \cap B)`

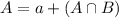
In which a represents those that participate in the work force but are not married and
`(A \cap B)` are those who are both on the work force and married.

By the same logic, we have that:

`B = b + (A \cap B)`

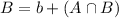
We start finding the values from the intersection of these sets:

Suppose also that 61% of women 25 through 49 years of age are married and are participating in the labor force.

This means that
`A \cap B = 0.61`

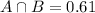
Suppose 78% of the women in that age group are married.

This means that
`B = 0.78`

`B = b + (A \cap B)`

`0.78 = b + 0.61`

`b = 0.17`

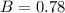
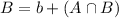
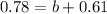
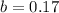
75% of the women 25 through 49 years of age participate in the labor force.

This means that
`A = 0.75`

`A = a + (A \cap B)`

`0.75 = a + 0.61`

`a = 0.14`

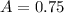
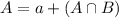
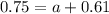
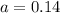
a. What is the probability that a randomly selected woman in that age group is married or is participating in the labor force

This is

`P = a + b + (A \cap B) = 0.14 + 0.17 + 0.61 = 0.92`

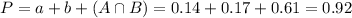
There is a 92% probability that a randomly selected woman in that age group is married or is participating in the labor force.

b. What is the probability that a randomly selected woman in that age group is married or is participating in the labor force but not both?

This is

`P = a + b`

`P = 0.14 + 0.17`

`P = 0.31`

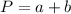
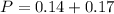
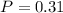
There is a 31% probability that a randomly selected woman in that age group is married or is participating in the labor force but not both.

c. What is the probability that a randomly selected woman in that age group is neither married nor participating in the labor force?

From a), we found that there is a 92% probability that a randomly selected woman in that age group is married or is participating in the labor force.

This means that there is an 8% probability that a randomly selected woman in that age group is neither married nor participating in the labor force.