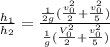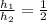Question

1. Two identical bowling balls of mass M and radius R roll side by side at speed v0 along a flat surface. Ball 1 encounters a ramp of angle θ that has a tacky surface and rolls up without slipping until it reaches a maximum height h1. Ball 2 encounters a ramp of angle θ that has a frictionless surface which it ascends to a maximum height h2. What is the ratio of h1/h2 in terms of M, v0, θ, g, and R?

Answer 1

1/2

Step-by-step explanation:

We need to make a couple of considerations but basically the problem is solved through the conservation of energy.

I attached a diagram for the two surfaces and begin to make the necessary considerations.

Rough Surface,

We know that force is equal to,

`F_r = mgsin\theta`

`F_r = \mu N`

`F_r = \mu mg cos\theta`

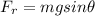
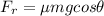
Matching the two equation we have,

`\mu N = \mu mg cos\theta`

`\mu = tan\theta`

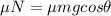
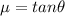
Applying energy conservation,

`(1)/(2)mv^2_0+(1)/(2)I_w^2 = F_r*d+mgh_1`

`(1)/(2)mv^2_0+(2)/(5)mR^2(V_0^2)/(R^2) = F_r*d+mgh_1`

`(1)/(2)mv^2_0+(mv_0^2)/(5) = mgsin\theta \frac{h_1sin\theta}+mgh_1`

`(v_0^2)/(2)+(v_0^2)/(5) = gh_1+gh_1`

`h_1 = (1)/(2g)((v_0^2)/(2)+(v_0^2)/(5))`

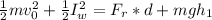
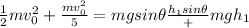
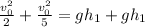
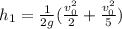
Frictionless surface

`(1)/(2)mv_0^2+(1)/(2)I\omega^2 = mgh_2`

`(1)/(2)m_v^2+(1)/(2)(2)/(5)mR^2(v_0^2)/(R^2) =mgh_2`

`(v_0^2)/(2)+(v_0^2)/(5) = gh_2`

`h_2 = (1)/(g)((V_0^2)/(2)+(v_0^2)/(5))`

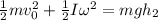
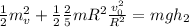
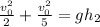
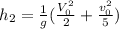
Given the description we apply energy conservation taking into account the inertia of a sphere. Then the relation between
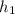`h_1` and
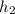`h_2` is given by

`(h_1)/(h_2) = ((1)/(2g)((v_0^2)/(2)+(v_0^2)/(5)))/((1)/(g)((V_0^2)/(2)+(v_0^2)/(5)))`

`(h_1)/(h_2) = (1)/(2)`