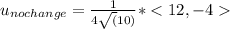Question

Consider the function f (x comma y )equals3 x squared minus 2 y squared minus 3 and the point (negative 2 comma 1 ). a. Find the unit vectors that give the direction of steepest ascent and steepest descent at P. b. Find a vector that points in a direction of no change in the function at P.

Answer 1

Answer: see description

Explanation:

given the function
`f(x,y) = 3x^2-2y^2-3`

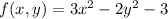
we calculate the gradient
`\\abla f(x,y) = (\partial f(x,y))/(\partial x) \hat{\textbf{x}}+ (\partial f(x,y))/(\partial y) \hat{\textbf{y}} + (\partial f(x,y))/(\partial z) \hat{\textbf{z}}`

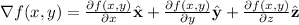
for each term we consider all variables different to the one we are derivating as constants. For each term we have

`(\partial f(x,y))/(\partial x) = 3 (\partial )/(\partial x)(x^2) = 6x\\ (\partial f(x,y))/(\partial y) = -2 (\partial )/(\partial x)(y^2) = -4y\\(\partial f(x,y))/(\partial z) = 0\\`

Therefore:

`\\abla f(x,y) = 6x \hat{\textbf{x}} -4y \hat{\textbf{y}}`

gives the direction of maxium increase.

a) with x = -2, y= 1

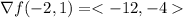`\\abla f(-2,1) = <-12,-4>` which magnitude is
`√((-12)^2+(-4)^2 ) = √(160) = 4 √(10)`

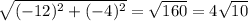
so the unitary vector in the direction of the steepest ascent is

`u_(1) = (\\abla f(-2,1))/(|\\abla f(-2,1)|) = (1)/(4 \sqrt(10))*<-12,-4>`

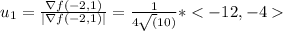
and the unitary vector in the direction of steepest descent is

`u_(2) = (- \\abla f(-2,1))/(|\\abla f(-2,1)|) = (1)/(4 \sqrt(10))*<12,4>`

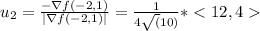
finally, the vector in no change direction is basically doing one of the following possibilities with
`u_(1)`:

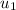if we have a vector <a,b> the perpendicular vector (direction of no change) will be either <-a,b> or <a,-b>

so i will select <-a,b>

`u_(no change) =  (1)/(4 \sqrt(10))*<12,-4>`