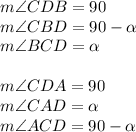Answer:
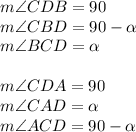
Explanation:
The triangles are drawn below.
CD is perpendicular to AB as CD is height to AB.
Therefore, angles
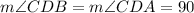 °
°
So, triangles ΔCBD and ΔCAD are right angled triangles.
Now, from the right angled triangle ΔABC,
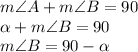
From ΔCBD,
 is same as
is same as
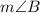 .
.
So,
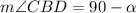

Now, from ΔCAD,
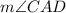 is same as
is same as
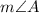
So,

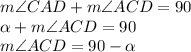
Hence, the unknown angles of both the triangles are: