Answer:
-
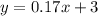
- The cost of surfing the web at the café for one hour:
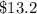
Explanation:
The equation of the line in Slope-Intercept form is:

Where "m" is the slope and "b" is the y-intercept.
Take two points and substitute them into the formula for calculate the slope (The formula is
 ).
).
Having these points:
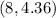 and
and
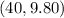
You can identify that:
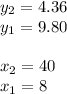
Then, the slope is:
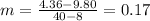
Substitute the slope and the coordinates of any point on the line into the equation
 and then solve for "b":
and then solve for "b":
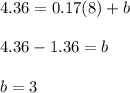
Therefore, equation in Slope-Intercept form that represents the function is:
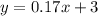
Since 1 hour hour has 60 minutes, you need to substitute
 into the equation and then evaluate, in order to find the cost of surfing the web at the café for one hour. Then:
into the equation and then evaluate, in order to find the cost of surfing the web at the café for one hour. Then:
