Question

You must design a closed rectangular box of width w, length l and height h, whose volume is 504 cm3. The sides of the box cost 3 cents/cm2 and the top and bottom cost 4 cents/cm2. Find the dimensions of the box that minimize the total cost of the materials used.

Answer 1

Dimensions will be

Length = 7.23 cm

Width = 7.23 cm

Height = 9.64 cm

Explanation:

A closed box has length = l cm

width of the box = w cm

height of the box = h cm

Volume of the rectangular box = lwh

504 = lwh

`h=(504)/(lw)`

Sides which involve length and width and height, cost = 3 cents per cm²

Top and bottom of the box costs = 4 cents per cm²

Cost of the sides
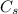`C_(s)`= 3[2(l + w)h] = 6(l + w)h

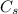`C_(s)`= 3[2(l + w)h]

`C_(s)=6(l+w)((504)/(lw) )`

Cost of the top and the bottom
`C_((t,p))`= 4(2lw) = 8lw

Total cost of the box C =
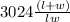`3024((l+w))/(lw)` + 8lw

=
`3024[(1)/(l)+(1)/(w)]` + 8lw

To minimize the cost of the sides

`(dC)/(dl)=3024(-l^(-2)+0)+8w=0`

`(3024)/(l^(2))=8w`

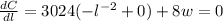
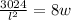
`(378)/(l^(2))=w` ---------(1)

`(dC)/(dw)=3024(-w^(-2))+8l=0`

`(3024)/(w^(2))=8l`

`(378)/(w^(2))=l`

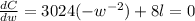
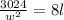
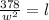
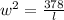`w^(2)=(378)/(l)`-------(2)

Now place the value of w from equation (1) to equation (2)

`((378)/(l^(2)))^(2)=(378)/(l)`

`((378)^(2) )/(l^(4))=(378)/(l)`

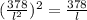
l³ = 378

l = ∛378 = 7.23 cm

From equation (2)

`w^(2)=(378)/(7.23)`

`w^(2)=52.28`

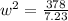
w = 7.23 cm

As lwh = 504 cm³

(7.23)²h = 504

`h=(504)/((7.23)^(2))`

h = 9.64 cm