Question

A string or rope will break apart if it is placed under too much tensile stress. Thicker ropes can withstand more tension without breaking because the thicker the rope, the greater the cross-sectional area and the smaller the stress. One type of steel has density 7890 kg/m3 and will break if the tensile stress exceeds 7.0×108N/m2. You want to make a guitar string from a mass of 4.0 g of this type of steel. In use, the guitar string must be able to withstand a tension of 900 N without breaking. Your job is to determine (a) the maximum length and minimum radius the string can have; (b) the highest possible fundamental frequency of standing waves on this string, if the entire length of the string is free to vibrate.

Answer 1

a. radius = 0.0006m = 0.6mm and length =0.393m = 393mm

b. frequency =377.86Hz

Step-by-step explanation:

Given:

mass of steel= 4g = 0.004kg

density of steel = 7890kg/m3

tensile stress of steel 7.0x10⁸

tension load =900N

from the density, we will calculate for the Volume of the steel string

density = mass/volume

volume = mass/density = 0.004/7890 = 5.07 x 10⁻⁷ m³

from the tensile stress will can get the maximum base Area of the string ,

tensile stress = load/area =

7x10⁸ = 900/A

A = 900/7x10⁸ = 1.29x10⁻⁶ m²

Area = πr²

area/pi = 4.105x10-7

radius = 0.0006m = 0.6mm

volume = Area x length

length = vol/area =(5.07 x 10⁻⁷ m³)/1.29x10⁻⁶ m² = 0.393m

b. the highest possible frequency is given by:

F =
`\frac{\sqrt{(T)/(m/L) }}{2L}`

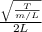
where T= tension, m=mass, L=length

F =
`\frac{\sqrt{(900)/(0.004kg/0.393m) }}{2*0.393m}`

= 297.04/0.786

frequency =377.86Hz