Question

A riverboat can sail 28 mph in calm waters. Sailing with the Gulf Stream, the boat can sail 170 miles in the same amount of time as it takes to sail 110 miles against the Gulf Stream. Find the rate of the Gulf Stream.

Answer 1

6 mph

Explanation:

If x is the rate of boat (given x = 28)

and c is the rate of Gulf Stream (we need to find this)

The rate downstream is with the current, that is

x+c

THe rate of upstream is against the current, that is

x-c

We also know D = RT

D is distance

R is rate

T is time

It takes same time, so we can say:

t = D/R

So we can equate both to:

`(170)/(x+c)=(110)/(x-c)\\(170)/(28+c)=(110)/(28-c)`

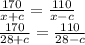
We can cross multiply this and solve for c:

`(170)/(28+c)=(110)/(28-c)\\170(28-c)=110(28+c)\\4760-170c=3080+110c\\1680=280c\\c=6`

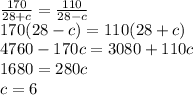
The speed of current (rate of Gulf Stream) = 6 miles per hour