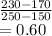Answer:
0.2,0.2,0.6
Explanation:
Given that a continuous random variable is uniformly distributed between 150 and 250.
We know that a uniform distribution between (a,b) has pdf as
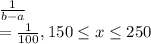
a) the probability a randomly selected value will be greater than 230
=
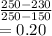
b) the probability a randomly selected value will be less than 170
=

c) the probability a randomly selected value will be between 170 and 230
=