Question

Bones Brothers & Associates prepare individual tax returns. Over prior years, Bones Brothers has maintained careful records regarding the time to prepare a return. The mean time to prepare a return is 90 minutes, and the population standard deviation of this distribution is 14 minutes. Suppose 100 returns from this year are selected and analyzed regarding the preparation time. What is the probability that the mean time for the sample of 100 returns for this year is greater than 92?

Answer 1

P(x>92) = 0.4431

Explanation:

Let X be a random variable which is a measure of the time to get returns.

Mean (u) = 90 mins

Standard deviation(α) = 14 mins

Number (n) = 100

For normal distribution

Z = (X - u) / α

For Pr(x = 92)

(92 - 90) / 14

= 2/14

= 0.143

From the normal distribution table 0.143 = 0.0569

Φ(α) = 0.0569

Recall that if Z positive,

Pr(x>a) = 0.5 -Φ(α)

Therefore;

Pr(x>92) = 0.5 - 0.0569

= 0.4431

Answer 2

Answer: 0.0764

Explanation:

Given : Population mean :
`\mu= 90\text{ minutes}`

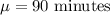
Standard deviation :
`\sigma = 14\text{ minutes}`

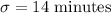
Let
`\overline{x}` be the mean time for the sample of 100 returns for this year.

Now , the probability that the mean time for the sample of 100 returns for this year is greater than 92 is given by :-

`P(\overline{x}>92)= P(\frac{\overline{x}-\mu}{(\sigma)/(√(n))}>(92-90)/((14)/(√(100))))\\\\=P(z>1.43)\ \ \ [\because\ z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}]\\\\= 1-P(z\leq1.43)\ \ \ [\because\ P(Z>z)=1-P(Z\leq z)]`

`=1-0.9236=0.0764`

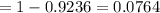
Hence, the required probability is 0.0764.