Answer:
(D) Standard error of the mean decreases, width of confidence interval becomes narrower.
Explanation:
Given that an analyst takes a random sample of 25 firms in the telecommunications industry and constructs a confidence interval for the mean return for the prior year.
When all others remain constant n increases from 25 to 30
Because of this std error becomes
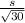
instead of
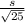
As a result standard error decreases and in turn margin of error also decreases.
Hence correct option would be
(D) Standard error of the mean decreases, width of confidence interval becomes narrower.