Question

A person of mass 70 kg stands at the center of a rotating merry-go-round platform of radius 2.9 m and moment of inertia 900 kg⋅m2 . The platform rotates without friction with angular velocity 0.95 rad/s . The person walks radially to the edge of the platform. Part APart complete Calculate the angular velocity when the person reaches the edge. Express your answer using three significant figures and include the appropriate units. ωω = 0.574 rads Previous Answers Correct Part B Calculate the rotational kinetic energy of the system of platform plus person before and after the person's walk.

Answer 1

Step-by-step explanation:

It is given that,

Mass of person, m = 70 kg

Radius of merry go round, r = 2.9 m

The moment of inertia,
`I_1=900\ kg.m^2`

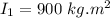
Initial angular velocity of the platform,
`\omega=0.95\ rad/s`

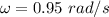
Part A,

Let
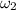`\omega_2` is the angular velocity when the person reaches the edge. We need to find it. It can be calculated using the conservation of angular momentum as :

`I_1\omega_1=I_2\omega_2`

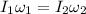
Here,
`I_2=I_1+mr^2`

`I_1\omega_1=(I_1+mr^2)\omega_2`

`900* 0.95=(900+70* (2.9)^2)\omega_2`

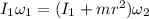
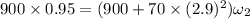
Solving the above equation, we get the value as :

`\omega_2=0.574\ rad/s`

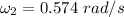
Part B,

The initial rotational kinetic energy is given by :

`k_i=(1)/(2)I_1\omega_1^2`

`k_i=(1)/(2)* 900* (0.95)^2`

`k_i=406.12\ rad/s`

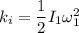
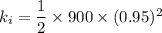
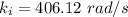
The final rotational kinetic energy is given by :

`k_f=(1)/(2)(I_1+mr^2)\omega_1^2`

`k_f=(1)/(2)* (900+70* (2.9)^2)(0.574)^2`

`k_f=245.24\ rad/s`

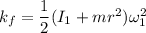
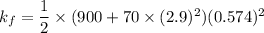
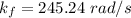
Hence, this is the required solution.