Question

write a variable expression to describe the rule for the sequence. Then find the 10th term. 15,13,11, 9..

Answer 1

The variable expression to describe the rule of sequence is
`T_(n)=17-2 n` And the 10th term is -3

Solution:

The given series is 15, 13, 11, 9 ….

The given series is arithmetic series with common difference "-2"

From the above series we get,

First term
`a_1 = 15`

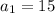
Second term
`a_2 = 13`

And so on.

Common difference =
`d = a_2 - a_1 = -2`

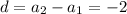
The nth term of Arithmetic progression is given as:

`\mathrm{T}_{\mathrm{n}}=\mathrm{a}_(1)+(\mathrm{n}-1) \mathrm{d}`

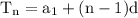
Where "a" is the first term of sequence

"n" is the nth term

"d" is common difference between terms

`\begin{array}{l}{T_(n)=15+(n-1) *(-2)} \\\\ {T_(n)=15-2 n+2} \\\\ {T_(n)=17-2 n}\end{array}`

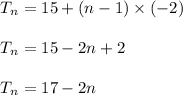
Which is the required variable expression to describe the rule for the given sequence

Finding 10th term:

Substitute n = 10 in above variable expressi
`T_(10) = 17 - 2(10) = 17 - 20 = -3`

Hence the 10th term is -3