Question

The area of a rectangular plank is 4500 cm². The plank was broken into two pieces, one of which is a square and the other a rectangle. Find the dimensions of the square if the length of the broken off rectangle is 120 cm.

Answer 1

`Xs=30cm` and
`As=900 cm^(2)`

Explanation:

At=As+Ar; A=b.h and
`At=4500 cm^(2)`, then: At=(x+120)x so

(x+120)x=4500,
`x^(2) +120x-4500=0` Applying cuadratic equation formula:
`\frac{120+-\sqrt{120^(2) -4.1.-4500} }{2} =-(120+-√(14400+18000) )/(2)= x1=30 and x2=-150, finally Xs=30cm, and As=900cm^(2)`

Answer 2

30cm

Explanation:

Let the dimensions of the square is x cm.

The plank of area 4500 cm² was broken into two pieces, one of which is a square and the other a rectangle.

Length of the broken off rectangle = 120 cm

Width of the broken off rectangle = x cm

Length of plank = (120+x) cm

Width of plank = x cm

Area of a rectangle is

`Area=lenght* width`

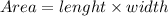
Area of plank is

`Area=(x+120)* x`

`Area=x^2+120x`

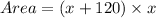
The area of a rectangular plank is 4500 cm².

`x^2+120x=4500`

`x^2+120x-4500=0`

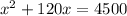
Splitting the middle term we get

`x^2+150x-30x-4500=0`

`x(x+150)-30(x+150)=0`

`(x+150)(x-30)=0`

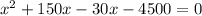
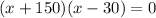
Using zero product property we get

`(x+150)=0\Rightarrow x=-150`

`(x-30)=0\Rightarrow x=30`

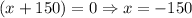
x can not be a negative number because it is the side length of square. So, x=30.

Therefore, the side length of the square is 30cm.