Question

In an examination of purchasing patterns of shoppers, a sample of 16 shoppers revealed that they spent, on average, $54 per hour of shopping. Based on previous years, the population standard deviation is thought to be $21 per hour of shopping. Assuming that the amount spent per hour of shopping is normally distributed, find a 90% confidence interval for the mean amount.

a. [$51.8409, $56.1591]
b. [$52.3174, $55.6826]
c. [$45.3637, $62.6363]
d. [$47.2695, $60.7305]

Answer 1

The 90% confidence interval is c) $45.3637, $62.6363

Step-by-step explanation:

Hi, since we need to find the Z value from the standard deviation table that would substract an equal area from both size of the normal distribution graph, we can tell that the probability that we have to rate into account is 5% (I mean, 10%, which we substract from both sides 5%), and the Z number for a probability of 5% is -1.645 which is the lower end of the interval, and due to symmetry, the higher end of the interval would be 1.645.

Now, we need to use the following formula in order to find the lower and higher ends of the interval.

`0.9C.L=Mean+1.645((StdDev)/(√(n) ))`

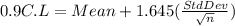
Where:

C.L = Confidence Level

Mean = in our case, $54

StdDev = $21

n = sample sizes, in our case, that would be 16

So, the lower level would be

`0.9C.L=54-1.645((21)/(√(16) ))`

`L.End=45.36375`

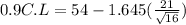
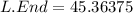
Therefore:

`0.9C.L=54+1.645((21)/(√(16) ))`

`H.End=62.63625`

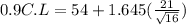
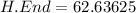
So, the interval in order to have 90% confidence is c. [$45.3637, $62.6363]