Question

Find the area of the triangles ABD and BCD using Heron’s formula. Hence find the area of quadrilateral ABCD.

Answer 1

The Area of quadrilateral ABCD is 36 cm²

Explanation:

Given in the figure as :

ABD and BCD is a triangle

Length of sides of Δ ABD is:

AD = 3 cm

AB = 4 cm

BD = x =
`\sqrt{(AB)^(2)+ (AD)^(2)}`

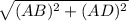
Or, BD =
`\sqrt{(4)^(2)+ (3)^(2)}` =
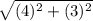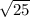`√(25)` = 5 cm

Length of sides of ΔCBD is :

BC = 13 cm

CD = 12 cm

Now By Heron's formula

Area of triangle ABD =
`√(s (s -a)(s-b) (s-c))`

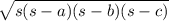
And s =
`(AB + BD +DA)/(2)`

Or, s =
`(4 + 5 +3)/(2)`

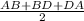
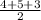
Or, s = 6 cm

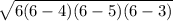
∴ Area of triangle ABD =
`√(6 (6 -4)(6-5) (6-3))`

Or, Area of triangle ABD =
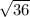`√(36)` = 6 cm²

Similarly The area of Triangle CBD =
`√(s (s -a)(s-b) (s-c))`

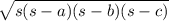
And s =
`(CB + BD +DC)/(2)`

Or, s =
`(13 + 5 +12)/(2)`

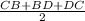
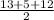
Or, s = 15 cm

∴ Area of triangle CBD =
`√(15 (15 -13)(15-5) (15-12))`

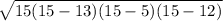
Or, Area of triangle CBD =
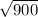`√(900)` = 30 cm²

The Area of quadrilateral ABCD = Area Δ ABD + Area Δ CBD

Or,The Area of quadrilateral ABCD = 6 cm² + 30 cm² = 36 cm²

Hence The Area of quadrilateral ABCD is 36 cm² Answer