Answer: 0.0025
Explanation:
Let
 be the population mean for the gasoline price of one of the major oil companies .
be the population mean for the gasoline price of one of the major oil companies .
As per given , we hav
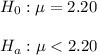
Since the alternative hypothesis is left-tailed , so the test is a left-tailed test.
Given : n= 36
Degree of freedom : 35 (df= n-1)
The given test statistic : t=-3
Using the p-value table or p-value calculator for a student's t -value left-test having degree of freedom 35, we have
P-value :
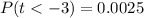
Thus , the required p-value = 0.0025