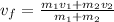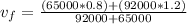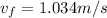Question

Consider the two moving boxcars in Example 5. Car 1 has a mass of m1 = 65000 kg and a velocity of v01 = +0.80 m/s. Car 2 has a mass of m2 = 92000 kg and a velocity of v02 = +1.2 m/s, overtakes car 1 and couples to it. Determine the velocity of their center of mass

(a) beforethe collision
(b) after the collision.

Answer 1

1.034m/s

Step-by-step explanation:

We define the two moments to develop the problem. The first before the collision will be determined by the center of velocity mass, while the second by the momentum preservation. Our values are given by,

`m_1 = 65000kg\\v_1 = 0.8m/s\\m_2 = 92000kg\\v_2 = 1.2m/s`

Part A) We apply the center of mass for velocity in this case, the equation is given by,

`V_(cm) = (m_1v_1+m_2v_2)/(m_1+m_2)`

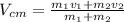
Substituting,

`V_(cm) = ((65000*0.8)+(92000*1.2))/(92000+65000)`

`V_(cm) = 1.034m/s`

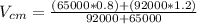
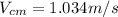
Part B)

For the Part B we need to apply conserving momentum equation, this formula is given by,

`m_1v_1+m_2v_2 = (m_1+m_2)v_f`

Where here
`v_f` is the velocity after the collision.

`v_f = (m_1v_1+m_2v_2)/(m_1+m_2)`

`v_f = ((65000*0.8)+(92000*1.2))/(92000+65000)`

`v_f = 1.034m/s`