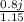Answer:
7. D
8. A
9. D
10. B
11 A)

11 B)
Explanation:
7.
Let Emmet work for "m" minutes
Since, Cal worked 4times as this, we can say Cal worked for "4m" minutes
Now, the total time (CAL + EMMET) is 720, so we SUM UP their individual times' expression and equate to 720. Shown below:
4m + m = 720
This is Answer choice D
8.
Let s be the price of each shirt
Each shirt costs "s" each, so 4 shirts cost "4s" in total.
4 shirts costs 60 AFTER 10 dollar discount, so before discount, it was:
60 + 10 = 70 dollars
Hence, 4 shirts cost 70 dollars BEFORE discount, so we can say:
4s = 70
But none of the choices are this, we need to simply manipulate this equation to get our answer (from choices).
How did we get 70? We added 60 and 10. So we can put "60" on the right hand side and "-10" on the left hand side to get:
4s - 10 = 60
This is ultimatley 4s = 70
So the correct answer choice is A
9.
Let Tony's age be "y"
We know grandmother is "3 years MORE than 6 times TONY (y)", thus we can write:
Grandmother is "6y + 3"
Total sum of them both is 87. Thus we can SUM both these expressions and equate to 87. Thus,
y + 6y + 3 = 87
D is the correct choice.
10.
THe total length is "f"
Each piece cut is 3/4
So the number of pieces is the total by each piece, so that is
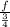
All these "number of pieces" makes 6 shelves (since he used all), so we equate this expression to "6". Now we have:

That is answer choice B
11 A)
Let Jocelyn's computer's price be "j",
Adrian's is 640, which is 20% LESS THAN Jocelyn's (j), so we can say:
640 is 20% less than "j"
or
"20% less than j" would be:
j - 0.2j = 0.8j
Now, we can write:
640 = 0.8j
11 B)
We can say:
Adrian is 15% more than Corbin
or
A = 0.15C + C
A = 1.15C
[note: let adrian's computer price be A and Corbin's computer price be C]
Also we know
0.8j = Adrian
We can put this in to get:
A = 1.15C
C = A/1.15
C = 0.8j/1.15
THis is an expression for Corbin's computer price in terms of j: