Question

1) A projectile is thrown upward so that its distance above the ground after t seconds is

h=-10t2 +440 t. After how many seconds does it reach its maximum height?​

Answer 1

After 22 seconds the projectile reach its maximum height of 4,840 units

Explanation:

we have

`h(t)=-10t^(2)+440t`

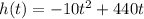
This is a vertical parabola downward (because the leading coefficient is negative)

The vertex is a maximum

Find out the coordinates of the vertex

Convert the quadratic equation in vertex form

Factor -10

`h(t)=-10(t^(2)-44t)`

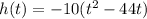
Complete the square

`h(t)=-10(t^(2)-44t+22^2)+(10)(22^2)`

`h(t)=-10(t^(2)-44t+22^2)+4,840`

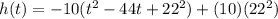
Rewrite as perfect squares

`h(t)=-10(t-22)^(2)+4,840`

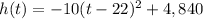
The vertex is the point (22,4,840)

therefore

After 22 seconds the projectile reach its maximum height of 4,840 units