Answer:
11.33 feet
Explanation:
The triangle for the given scenario is drawn below.
From the triangle ΔABC, AB is the length of the ladder, B is the foot of the ladder, AC is the wall, BC is the distance of the foot from the wall, and angle B is the angle of elevation of the ladder with ground.
Let the length of the ladder,
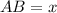
As per question, BC = 6.5 ft,
 °
°
Using cosine ratio of the angle B, we get

Therefore, the length of the ladder is 11.33 ft.