Answer:
P( The distance is at most 100 m) = 0.7499263989
P( The distance is at most 200 m) = 0.937463194
Explanation:
For the banner-tailed Kangaroo rats, X has an exponential distribution with parameter
 = 0.01386
= 0.01386
So, probability distribution of X is given by,
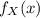 =
=
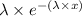
for 0 ≤ x < ∞ where
 = 0.01386
= 0.01386
= 0 otherwise
so,
P( X ≤ 100) =
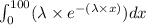
=
![[- e^(-x * \lambda)]_(0)^(100)](https://img.qammunity.org/2020/formulas/mathematics/college/6252jvyz8eosye2gb97a0zuzy9dctzw3nb.png) ----------------(2)
----------------(2)
=1 -

= 0.7499263989
so , P(X ≤ 200)
= 1 -
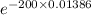
= 0.937463194
=