Question

An irregularly-shaped object of length 9.2 m is placed with each end on a scale. If the scale on the right reads 73 N and the one on the left reads 91 N , how far from the left is the object's center of gravity?

Answer 1

5.1 m

Step-by-step explanation:

from the question we are given the following:

length of the object (L) = 9.2 m

weight on the right scale (Wr) = 73 N

weight on the left scale (Wl) = 91 N

position of the center of gravity (CG) from the left = ?

We can get the position of the center of gravity (CG) by finding the net torque about the center of gravity (CG).

Take note of the following:

• From the diagram below the distance of the right end from the center of gravity (CG) is taken as P.
• The distance of the center of gravity (CG) from the left end is the total length - P = 9.2 - P
• Since the object id not moving about its center of gravity (CG) , its net torque about the center of gravity (CG) is zero

therefore taking the clockwise direction as positive the equation for the net torque about the center of gravity (CG) will be

(Wr x P) - (Wl x (9.2 - P)) = 0

(Wr x P) = (Wl x (9.2 - P))

P =
`((Wr x 9.2))/(WR + Wl)`

P =
`((73 x 9.2))/(73 + 91)`

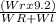
P= 4.1 m

Recall that the distance of the center of gravity (CG) from the left end is the total length - P = 9.2 - P

= 9.2 - 4.1 = 5.1 m