Answer:
The length of he hypotenuse of the triangle is x = 65.
Explanation:
Here, the base of the right triangle = 56
The perpendicular = 33
The hypotenuse of the triangle = x
Now, by PYTHAGORAS THEOREM: In a right angled triangle
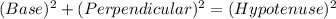
or, here
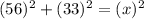
or,
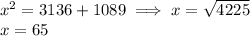
Hence, the length of he hypotenuse of the triangle is 65.