Question

Find the value of x in the triangle

Answer 1

55.52°

Step-by-step explanation:

Concept tested: Sine rule of triangles

We need to know the sine rule

• According to sine rule, if the three sides of a triangle are a, b and c and the corresponding angles, A, B and C

• Then,
  `(a)/(SinA)=(b)/(SinB)=(c)/(SinC)`

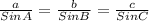
In this case;

• If we take, a = 5.7 units and A = 70°, and

b= 5 units, B = x°

• Using the sine rule we can find the value of x

Therefore;

`(a)/(SinA)=(b)/(SinB)`

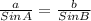
Then;

`(5.7)/(Sin70)=(5)/(Sinx)`

`6.0658=(5)/(sinx)`

`Sinx=0.8243`

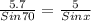
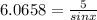
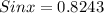
Therefore, X = 55.52°

Therefore, the value of x in the triangle is 55.52°