Answer:
Part c)
The Slope of the line is: m=-50 and represents the amount of money spent per week.
Part d)
The y-intercept is: c=300 and represents the maximum money we have that can be spend over the weeks (i.e. our maximum budget alowed).
Explanation:
To solve this question we shall look at linear equations of the simplest form reading:
 Eqn(1).
Eqn(1).
where:
 : is our dependent variable that changes as a function of x
: is our dependent variable that changes as a function of x
 : is our independent variable that 'controls' our equation of y
: is our independent variable that 'controls' our equation of y
 : is the slope of the line
: is the slope of the line
 : is our y-intercept assuming an
: is our y-intercept assuming an
 ⇔
⇔
 relationship graph.
relationship graph.
This means that as
 changes so does
changes so does
 as a result.
as a result.
Given Information:
Here we know that $300 is our Total budget and thus our maximum value (of money) we can spend, so with respect to Eqn (1) here:
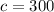
The budget of $50 here denotes the slope of the line, thus how much money is spend per week, so with respect to Eqn (1) here:
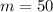
So finally we have the following linear equation of:
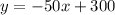 Eqn(2).
Eqn(2).
Notice here our negative sign on the slope of the line. This is simply because as the weeks pass by, we spend money therefore our original total of $300 will be decreasing by $50 per week.
So with respect to Eqn(2), and different weeks thus various
 values we have:
values we have:
Week 1:
 we have
we have
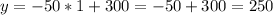 dollars.
dollars.
Week 2:
 we have
we have
 dollars.
dollars.
Thus having understood the above we can comment on the questions asked as follow:
Part c)
The Slope of the line is:
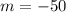 and represents the amount of money spent per week.
and represents the amount of money spent per week.
Part d)
The y-intercept is:
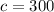 and represents the maximum money we have that can be spend over the weeks (i.e. our maximum budget alowed).
and represents the maximum money we have that can be spend over the weeks (i.e. our maximum budget alowed).