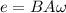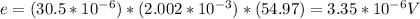Question

You toss a conductive open ring of diameter d=5.05 cmd=5.05 cm up in the air. The ring is flipping around a horizontal axis at a rate of 8.75 flips8.75 flips per second. One flip is a full rotation. At your location, the earth's magnetic field is Be=30.5 μT. What is the maximum emf induced in the ring?

Answer 1

`3.35 * 10^(-6)V`

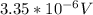
Step-by-step explanation:

Our values are given by,

`N = 8.75` flips per second

`d_1 = 5.05 * 10 ^ {2}m`

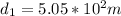
B = 30.5 µT

Directly through the number of flips we can find the angular velocity, that is,

`\omega = 2 \ piN`

`\omega = 2 \pi (8.75) = 54.97rad / s`

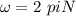
On the other hand, for the production of the electromotive force it is necessary to resort to the equation that relates to the magnetic field, angular velocity and area. The equation is given by,

`e = BA \omega`

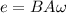
Where,

B = magnetic field

A = Area

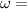`\omega =`Angular Velocity

In this way,

`Area = (\pi / 4) * (5.05 * 10^(-2))^2 = 2.002 * 10^(-3) m2`

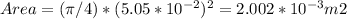
Applying the formula to find the emf, we replace,

`e = BA\omega`

`e = (30.5 * 10^(-6)) * (2.002 * 10^(-3)) * (54.97) = 3.35 * 10^(-6)V`