Question

My question that I'm suppose the answer is: Two particles, A and B, are in uniform circular motion about a common center. The acceleration of particle A is 6.0 times that of particle B. Particle B takes 2.4 times as long for a rotation as particle A. What is the ratio of the radius of the motion of particle A to that of particle B?

The options are:

5:1

1:3

14:1

1:1

I'm very confused here because I don't understand how any of these choices can represent the answer. I know the acceleration of A is 6 times greater than B, and B takes 2.4 times longer to to complete a rotation compared to A. But how can I compare the motions, when it doesn't really give me anything to compare it to?

Answer 1

Step-by-step explanation:

1:1 because the radius is common that means they are of the same radius just different acceleration

Answer 2

The ratio of the radius of the motion of particle A to that of particle B is 1:1

Solution:

Let v be the uniform circular motion,
`v=(2 * 3.14 * R)/(T) \rightarrow(1)`

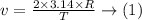
centripetal acceleration be
`a=(v^(2))/(R) \rightarrow(2)`

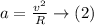
On substituting 1 in 2 we get,
`a=(\left[(2 * 3.14 * R)/(T)\right]^(2))/(R)=(2 * 3.14 * R)/(T^(2)) \rightarrow (3)`

Given, acceleration of A = 6x; B = x Time taken by A = t ; B = 2.4t For particle A, substituting the values,

`\begin{array}{l}{\Rightarrow 6 x=(2 * 3.14 * R)/(t^(2))} \\\\ {\Rightarrow 6 x=(6.28 R)/(t^(2))} \\\\ {\Rightarrow R=(6)/(6.28) * x t^(2)} \\\\ {\Rightarrow R a=0.955 x t^(2)}\end{array}`

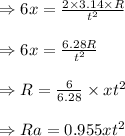
For particle B, substituting the values,

`\begin{array}{l}{\Rightarrow x=2 * 3.14 * (R)/((2.4 t)^(2))} \\\\ {\Rightarrow x=(6.28)/(5.76) * (R)/(t^(2))} \\\\ {\Rightarrow R=(5.76)/(6.28) * x t^(2)} \\\\ {R b=0.917 x t^(2)}\end{array}`

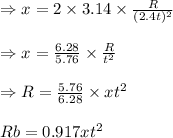
Therefore, the ratio of radii of A and B is Ra : Rb = 0.955 : 0:917 Approximately, it can be written as 1:1.