Question

The automobile assembly plant you manage has a Cobb-Douglas production function given by p = 10x^0.2 y^0.8

where P is the number of automobiles it produces per year, x is the number of employees, and y is the daily operating budget (in dollars). Assume that you maintain a constant work force of 130 workers and wish to increase production in order to meet a demand that is increasing by 100 automobiles per year. The current demand is 1200 automobiles per year. How fast should your daily operating budget be increasing? HINT [See Example 4.] (Round your answer to the nearest cent.)

= ? $ per yr

Answer 1

The variation needed for the daily buget to follow the increase in production for the first year is 12.38 $/year.

This value of Δy is not constant for a constant increase in production.

Explanation:

We know that the production function is
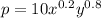`p = 10x^(0.2) y^(0.8)`, and in the current situation
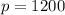`p=1200` and
`x=130`.

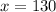With this information we can calculate the actual budget level:

`p_0 = 10x^(0.2) y^(0.8)\\\\1200=10*130^(0.2) y^(0.8)\\\\1200=26.47*y^(0.8)\\\\y=(1200/26.47)^(1/0.8)=45.33^(1.25)=117.62`

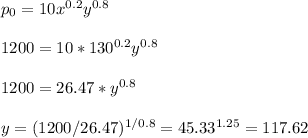
The next year, with an increase in demand of 100 more automobiles, the production will be
`p_1=1300`.

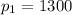If we calculate y for this new situation, we have:

`y_1=((p_1)/(10x^(0.2)) )^(1.25)=((1300)/(26.47) )^(1.25)=49.10^(1.25)=130`

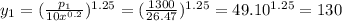
The budget for the following year is 130.

The variation needed for the daily buget to follow the increase in production for the first year is 12.38 $/year.

`\Delta y=y_1-y_0=130.00-117.62=12.38`

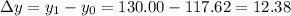
This value of Δy is not constant for a constant increase in production.