Answer:
The required probability is 0.0004995
Explanation:
Consider the provided information
There are 14 horses and one person owns 5 of those horses.
We need to find the number of ways in which 5 horses finish first, second , third, fourth, and fifth.
Each horse has the same probability of winning,
Therefore, the required probability is:
The probability that one of those 5 horses will be first is
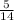
Now we have 4 horses left,
Probability that out of remaining 4 horses one will be second is
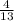 .
.
The probability that out of remaining 3 horses one will be third is
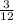 .
.
The probability that out of remaining 2 horses one will be fourth is
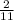 .
.
The probability that out of remaining 1 horses one will be fifth is
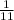 .
.
Hence, the total probability is:
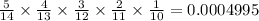
Hence, the required probability is 0.0004995