Question

Kim has a strong first​ serve; whenever it is good​ (that is,​ in) she wins the point 70​% of the time. Whenever her second serve is​ good, she wins the point 40​% of the time. Fifty dash five percent of her first serves and 70​% of her second serves are good. ​(a) What is the probability that Kim wins the point when she​ serves? ​(b) If Kim wins a service​ point, what is the probability that her 1st serve was​ good?

Answer 1

a) There is a 63.35% probability that Kim wins the point when she serves.

b) If Kim wins a service​ point, there is a 55.80% probability that her 1st serve was​ good.

Explanation:

We have these following probabilities

A 50.5% probability that her first serve is good.

A 70% probability that her second serve is good.

If her first serve is good, she has a 70% probability of winning the point.

If her second serve is good, a 40% probability of winning the point.

​(a) What is the probability that Kim wins the point when she​ serves?

This is the sum of 70% of 50.5% and 40% of 70%. So

`P = 0.7*(0.505) + 0.4*(0.7) = 0.6335`

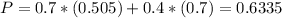
There is a 63.35% probability that Kim wins the point when she serves.

​(b) If Kim wins a service​ point, what is the probability that her 1st serve was​ good?

This can be formulated as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula

`P = (P(B).P(A/B))/(P(A))`

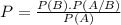
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

So

What is the probability of Kim's first serve being good, given that she won the point?

P(B) is the probability of Kim's first serve being good. So
`P(B) = 0.505`.

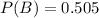P(A/B) is the probability of Kim's winning the point when her first serve is good. So
`P(A/B) = 0.70`.

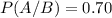P(A) is the probability of Kim's winning the point. From a), that is
`P(A) = 0.6335`

`P = (P(B).P(A/B))/(P(A)) = P = (0.505*0.70)/(0.6335) = 0.5580`

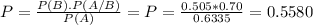
If Kim wins a service​ point, there is a 55.80% probability that her 1st serve was​ good.