Question

An article in the National Geographic News ("U.S. Racking Up Huge Sleep Debt," February 24, 2005) argues that Americans are increasingly skimping on their sleep. A researcher in a small Midwestern town wants to estimate the mean weekday sleep time of its adult residents. He takes a random sample of 80 adult residents and records their weekday mean sleep time as 6.4 hours. Assume that the population standard deviation is fairly stable at 1.8 hours. Use Table 1.

a.
Calculate a 95% confidence interval for the population mean weekday sleep time of all adult residents of this Midwestern town. (Round intermediate calculations to 4 decimal places, "z" value and final answers to 2 decimal places.)



Confidence interval to


b.
Can we conclude with 95% confidence that the mean sleep time of all adult residents in this Midwestern town is not 7 hours?

Yes, since the confidence interval contains the value 7.
Yes, since the confidence interval does not contain the value 7.
No, since the confidence interval contains the value 7.
No, since the confidence interval does not contain the value 7.

Answer 1

a)6 hours is the time to achieve 95% confidence level for the population.

b)Yes, because the confidence interval does not have the value 7

Answer 2

a) The 95% confidence interval for the population mean weekday sleep time of all adult residents of this Midwestern town is (6.01 hours, 6.74 hours).

b) Yes, since the confidence interval does not contain the value 7.

Explanation:

In the question a, we calculate the 95% confidence interval.

a)

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1-0.95)/(2) = 0.025`

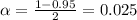
Now, we have to find z in the Ztable as such z has a pvalue of
`1-\alpha`.

So it is z with a pvalue of
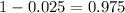`1-0.025 = 0.975`, so
`z = 1.96`

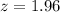
Now, find M as such

`M = z*(\sigma)/(√(n))  = 1.96*(1.8)/(√(80)) = 0.3944`

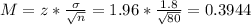
The lower end of the interval is the mean subtracted by M. So it is 6.4 - 0.3944 = 6.01 hours.

The upper end of the interval is the mean added to M. So it is 6.4 + 0.3944 = 6.74 hours.

The 95% confidence interval for the population mean weekday sleep time of all adult residents of this Midwestern town is (6.01 hours, 6.74 hours).

b.

Can we conclude with 95% confidence that the mean sleep time of all adult residents in this Midwestern town is not 7 hours?

The 95% confidence interval does not contain 7 hours, so the correct answer is

Yes, since the confidence interval does not contain the value 7.