Question

. The manager of a local small bank wants to estimate the average daily balance of all the checking accounts. Assume a random sample of 21 checking accounts at the bank are chosen, which shows an average daily balance of $303 and a standard deviation of $63. Assume that the underlying population of daily balance of all the checking accounts is normally distributed. Construct and interpret a 95% confidence interval estimate of the population mean (average) daily balance of all the checking accounts.

Answer 1

A 95% confidence interval estimate of the population mean (average) daily balance of all the checking accounts is $274.32 to $331.68

Explanation:

Consider the provided information.

A random sample of 21 checking accounts at the bank are chosen,

That means n=21

df = n-1

df = 21-1=20

We need to Construct and interpret a 95% confidence interval.

Determine t critical value for 95% confidence interval.

0.95=1-α

α=0.05

The sample size is small and it is a two tailed test.

From the t value table confidence interval is 2.086

An average daily balance is $303 and a standard deviation of $63.

`CI=\bar x\pm t_c * (s)/(√(n))`

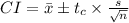
Substitute the respective values.

`CI=303\pm 2.086 * (63)/(√(21))`

`CI=303\pm 28.68`

`CI=274.32\ or\ 331.68`

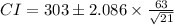
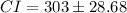
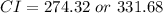
A 95% confidence interval estimate of the population mean (average) daily balance of all the checking accounts is $274.32 to $331.68