Question

According to Moebs Services Inc., an individual checking account at U. S. community banks costs these banks between $175 and $200 per year. Suppose that the average annual cost of all such checking accounts at U. S. community banks is $190 with a standard deviation of $20. Find the probability that the average annual cost of a random sample of 100 such checking accounts at U.S. community banks is

Answer 1

0.1855

Explanation:

Assuming normal distribution, Sampling mean = $190

Sampling standard deviation =
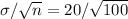`\sigma /√(n) = 20 /√(100)` = $2

a) Probability that the average annual cost of a random sample of 100 such checking accounts at U.S. community banks is less than $187 = P(X < 187)

= P(Z < (187 - 190)/2)

= P(Z < -1.5)

= 0.0668

b) Probability that the average annual cost of a random sample of 100 such checking accounts at U.S. community banks is more than $193.5

= 1 - P(X < 193.5)

= 1 - P(Z < (193.5 - 190)/2)

= 1 - P(Z < 1.75)

= 1- 0.9599

= 0.0401

c) Probability that the average annual cost of a random sample of 100 such checking accounts at U.S. community banks is between $191.70 to 194.5 = P(X < 194.5) - P(X <191.7)

= P(Z < (194.5 - 190)/2) - P(Z < (191.7-190)/2)

= P(Z < 2.25) - P(Z < 0.85)

= 0.9878 - 0.8023

= 0.1855