Question

We can model a pine tree in the forest as having a compact canopy at the top of a relatively bare trunk. Wind blowing on the top of the tree exerts a horizontal force, and thus a torque that can topple the tree if there is no opposing torque. Suppose a tree's canopy presents an area of 9.0 m2 to the wind centered at a height of 7.0 m above the ground. (These are reasonable values for forest trees.) If the wind blows at 6.5 m/s, what is the magnitude of the drag force of the wind on the canopy? Assume a drag coefficient of 0.50 and the density of air of 1.2 kg/m^3

What torque does this force exert on the tree, measured about the point where the trunk meets the ground?

Answer 1

114.075 N

798.525 Nm

Step-by-step explanation:

C = Drag coefficient = 0.5

ρ = Density of air = 1.2 kg/m³

A = Surface area = 9 m²

v = Velocity of wind = 6.5 m/s

r = Height of the tree = 7 m

Drag equation

`F=(1)/(2)\rho CAv^2\\\Rightarrow F=(1)/(2)* 1.2* 0.5* 9* 6.5^2\\\Rightarrow F=114.075\ N`

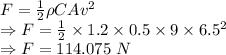
Magnitude of the drag force of the wind on the canopy is 114.075 N

Toque is given by the product of force and radius

`\tau=F* r\\\Rightarrow \tau=114.075* 7\\\Rightarrow \tau=798.525\ Nm`

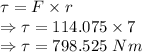
Torque exerted on the tree, measured about the point where the trunk meets the ground is 798.525 Nm