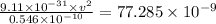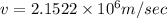Question

In the Bohr theory of the hydrogen atom, an electron moves in a circular orbit about a proton, where the radius of the orbit is approximately 0.546 ✕ 10-10 m. (The actual value is 0.529 ✕ 10-10 m.) (a) Find the electric force between the two, based on the approximate (not actual) radius given. 7.739e-8 Correct: Your answer is correct. N (b) If this force causes the centripetal acceleration of the electron, what is the speed of the electron? 8.495e22 Incorrect: Your answer is incorrect. m/s

Answer 1

(a) Electric force will be
`77.285* 10^(-9)N`

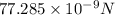
(B) Velocity
`v=2.1522* 10^6m/sec`

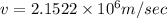
Step-by-step explanation:

We have given that radius of the circular orbit
`r=0.546* 10^(-10)m`

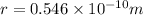
Charge on electron
`e=1.6* 10^(-19)C`

(A) According to coulomb's law electric force between two charges is given by

`F=(kq)/(r^2)`

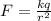
So electric force
`F=(9* 10^9* (1.6* 10^(-19))^2)/((0.546* 10^(-10))^2)=77.285* 10^(-9)N`

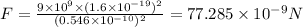
We know that centripetal force is given by
`F=(mv^2)/(r)`

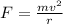
So
`(9.11* 10^(-31)* v^2)/(0.546* 10^(-10))=77.285* 10^(-9)`

`v=2.1522* 10^6m/sec`