Question

An RLC series circuit has a 2.60 Ω resistor, a 120 µH inductor, and an 88.0 µF capacitor. (a) Find the power factor at f = 120 Hz. 0.067 Correct: Your answer is correct. (b) What is the phase angle (in degrees) at 120 Hz? 3.29 Incorrect: Your answer is incorrect. °

Answer 1

Step-by-step explanation:

It is given that,

Resistance of the resistor, R = 2.6 ohms

Inductance,
`L=120\ \mu H=120* 10^(-6)\ H`

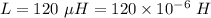
Capacitance,
`C=88\ \mu F=88* 10^(-6)\ F`

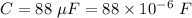
Frequency, f = 120 Hz

(a) The power factor of the series RLC circuit is given by :

`P=(R)/(Z)`

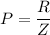
Z is the impedance of the LCR circuit.

Z is given by :

`Z=√(R^2+(X_L-X_C))`

`Z=√(R^2+(2\pi f L-1/2\pi f C))`

`Z=\sqrt{2.6^2+(2\pi * 120* 120* 10^(-6)-(1)/(2\pi * 120* 88* 10^(-6)))^2}`

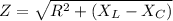
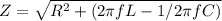
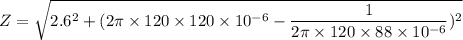
Z = 15.204 ohms

The power factor is given by :

`P=(2.6)/(15.204)`

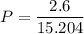
P = 0.171

The power factor of the series LCR series circuit is 0.171

(b) The phase angle is given by :

`cos\theta=(R)/(Z)`

`\theta=cos^(-1)((R)/(Z))`

`\theta=cos^(-1)(0.171)`

`\theta=80.154^(\circ)`

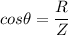
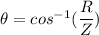
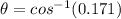
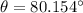
Hence, this is the required solution.