Question

Triangle X Y Z is shown. Angle X Z Y is a right angle. Angle Z X Y is 60 degrees and angle X Y Z is 30 degrees. The length of hypotenuse X Y is 42 and the length of X Z is 21.

Given right triangle XYZ, what is the value of tan(60°)?

One-half
StartFraction StartRoot 3 EndRoot Over 2 EndFraction
StartRoot 3 EndRoot
StartFraction 2 Over 1 EndFraction

Answer 1

The Answer is C.

Explanation:

Answer 2

Option C)
`\tan 60^\circ = \sqrt3`

Explanation:

We are given the following in the question:

A right angled triangle XYZ.

`\angle XZY = 90^\circ\\\angle ZXY = 60^\circ\\\angle XYZ = 30^\circ`

Length of hypotenuse XY = 42

Length of XZ = 21.

The right angle triangle follows or satisfy the Pythagoras theorem

• The Pythagoras theorem states that the hypotenuse is the longest side of a right angles triangle and that the sum of square of both the sides of the right angles triangle is equal to the square of the hypotenuse.

Thus, we can write:

`(\text{Side 1})^2 + (\text{Side 2})^2 = (\text{Hypotenuse})^2`

Putting the values, we get,

`(XZ)^2 + (ZY)^2 = (XY)^2\\(21)^2 + (ZY)^2 = (42)^2\\(ZY)^2 = 1764 - 441 = 1323\\ZY = √(1323) = 21√(3)`

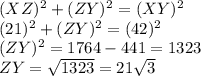
Now, we define,

`\bold{\tan \theta} = \displaystyle\frac{\text{Perpendicular}}{\text{Base}}`

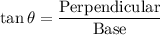
where the perpendicular and base are in accordance with the angle
`\theta`

Putting the values, we:

`\tan 6 0^\circ = \displaystyle(ZY)/(XZ) = (21\sqrt3)/(21) = \sqrt3`

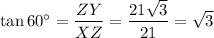
Option C)
`\tan 60^\circ = \sqrt3`