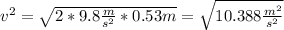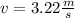Answer:
v=3.22 m/s
Step-by-step explanation:
This work is stored as gravitational potential energy. When Betty moves through the lowest position, that gravitational potential energy is converted to kinetic energy
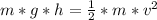
Resolve to v' so:
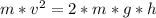
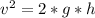
Now height is difference of both alture so
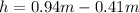
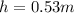
replacing