For this case we must solve the following equation:
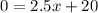
We know that:
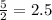
Rewriting the equation we have:
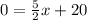
Subtracting 20 from both sides of the equation we have:
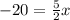
Multiplying by 2 on both sides of the equation we have:
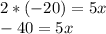
Dividing by 5 to both sides of the equation we have:
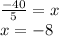
Thus, the value of "x" is -8.
Answer:
