Answer:
The solution to the equation
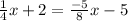 is
is
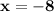
Option A is correct option.
Explanation:
What is the solution to the equation
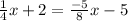
Solving the equation
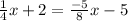
Subtracting 2 on both sides
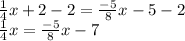
Adding 5/8x on both sides
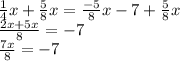
Multiply both sides by 8/7
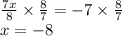
So, we get x = -8
The solution to the equation
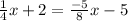 is
is
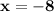
Option A is correct option.