Answer:
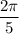 inches.
inches.
Explanation:
What is the circumference of this circle? The question states that radius
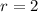 inches.
inches.
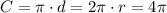 .
.
A full circle is similar to a sector of
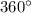 . The
. The
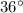 sector here will be a
sector here will be a
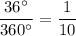 slice of the entire circle. Its arc length will be equal to
slice of the entire circle. Its arc length will be equal to
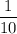 the circumference of the full circle. That's
the circumference of the full circle. That's
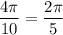 inches.
inches.