Question

The enthalpy of vaporization of a certain liquid is found to be 14.4 kJ mol-1 at 180 K, its normal boiling point. The molar volumes of the liquid and the vapour at the boiling point are 115 cm3 mol-1 and 14.5 dm3 mol-1, respectively. (a) Estimate dp/dT from the Clapeyron equation and (b) the percentage error in its value if the Clausius–Clapeyron equation is used instead.

Answer 1

(a) The value of
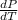`(dP)/(dT)` is
`5.56* 10^3Pa/K`

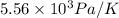
(b) The percentage error will be 2.5 %

Explanation :

(a) First we have to calculate the
`V_(vap)`.

`V_(vap)=V_2-V_1`

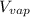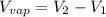
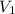`V_1` = volume of liquid =
`115cm^3mol^(1-)=115* 10^(-6)m^3mol^(1-)`

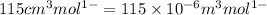
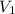`V_1` = volume of vapor =
`14.5dm^3mol^(1-)=14.5* 10^(-3)m^3mol^(1-)`

`V_(vap)=V_2-V_1`

`V_(vap)=(14.5* 10^(-3)m^3mol^(1-))-(115* 10^(-6)m^3mol^(1-))`

`V_(vap)=1.44* 10^(-2)m^3mol^(1-)`

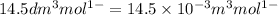
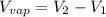
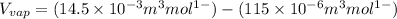
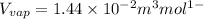
Now we have to calculate the value of
`(dP)/(dT)`

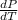
The Clausius- Clapeyron equation is :

`(dP)/(dT)=(\Delta H_(vap))/(T\Delta V_(vap))`

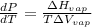
where,

T = temperature = 180 K

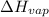`\Delta H_(vap)` = heat of vaporization = 14.4 kJ/mole = 14400 J/mole

`V_(vap)=1.44* 10^(-2)m^3mol^(1-)`

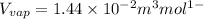
Now put all the given values in the above formula, we get:

`(dP)/(dT)=((14400J/mole))/((180K)* (1.44* 10^(-2)m^3mol^(1-)))* (1Pa)/(1J/m^3)`

`(dP)/(dT)=5.56* 10^3Pa/K`

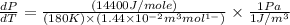
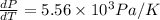
(b) Now we have to calculate the percentage error.

Now we have to calculate the value of
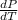`(dP)/(dT)` at normal boiling point.

The Clausius- Clapeyron equation is :

`(dP)/(dT)=(\Delta H_(vap))/(T\Delta V_(vap))`

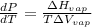
As we know that : PV = nRT

So,

`(dP)/(dT)=(P\Delta H_(vap))/(RT^2)`

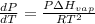
where,

R = gas constant = 8.314 J/K.mol

T = temperature = 180 K

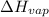`\Delta H_(vap)` = heat of vaporization = 14.4 kJ/mole = 14400 J/mole

P = pressure at normal boiling point = 101325 Pa

Now put all the given values in the above formula, we get:

`(dP)/(dT)=\frac{(101325Pa}* (14400J/mole)}{(8.314J/K.mol)* (180K)^2}`

`(dP)/(dT)=5.42* 10^3Pa/K`

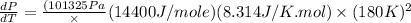
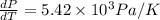
Now we have to determine percentage error.

`\%\text{ error}=((5.56* 10^3Pa/K)-(5.42* 10^3Pa/K))/(5.56* 10^3Pa/K)* 100`

`\%\text{ error}=2.5\%`

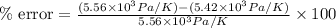
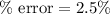
Therefore, the percentage error will be 2.5 %