Question

Review 1: A plane is located x = 40 miles (horizontally) away from an airport at an altitude of h miles. Radar at the airport detects that the distance s(t) between the plane and airport is changing at the rate of s(t) = −240 mph. If the plane flies toward the airport at the constant altitude h = 4, what is the speed |x(t)| of the airplane?

Answer 1

Step-by-step explanation:

Let h is the height of the plane above ground. x is the horizontal distance between the ground and the airport. Let s(t) is the distance between the plane and the airport. So,

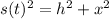`s(t)^2={h^2+x^2}`...........(1)

Given, h = 4, x = 40 and s(t) = -20 mph

Differentiate equation (1) wrt t

`2s(t)s'(t)=2x(t)x'(t)`

`x'(t)=(s(t)s'(t))/(x(t))`

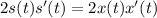
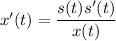
When x = 40,
`s(t)=√(40^2+4^2)=40.19\ m`

`x'(t)=(-240s(t))/(x(t))`

`x'(t)=(-240* 40.19)/(40)`

`x'(t)=-241.14\ m/s`

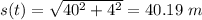
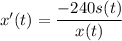
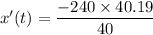
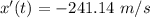
So, the speed of the airplane is 241.14 m/s. Hence, this is the required solution.