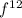Question

Choose the correct simplification of the expression f4 • f8.

Answer 1

Question

Choose the correct simplification of the expression
`f^(4) * f^(8)`

Answer:

`f^(4) * f^(8)` =
`f^(12)`

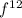
Explanation:

Topic: Indices

There are two methods of doing this;

Method 1

`f^(4) * f^(8)` ----- Expand both indices

=
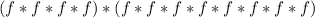`(f * f * f * f) * (f * f * f * f * f * f * f * f)` -- The total number of f is 12, so we have

=
`f^(12)`

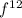
So,
`f^(4) * f^(8) = f^(12)`

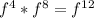
This method is not advisable when dealing with a large indices; hence, the need for method 2.

Method 2

Applying law of indices;

The first law of indices

The first law of indices states:
`a^(m) * a^(n) = a^(m+n)`.

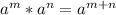This means that when numbers in index form with the same base are multiplied by each other, the powers (indices) are added together.

Applying this law on
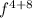
`f^(4) * f^(8)`

`f^(4) * f^(8)` =
`f^(4 + 8)`

`f^(4) * f^(8)` =
`f^(12)`