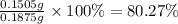Question

The metal content of iron in ores can be determined by a redox procedure in which the sample is first oxidized with Br2 to convert all the iron to Fe3+ and then titrated with Sn2+ to reduce the Fe3+ to Fe2+.

The balanced equation is: 2Fe3+(aq) + Sn2+(aq) -> 2Fe2+(aq) + Sn4+(aq)

What is the mass percentage Fe in a 0.1875g sample if 13.28 mL of 0.1015 M Sn2+ solution is needed to titrate the Fe3+?

Answer 1

80.27%

Step-by-step explanation:

Let's consider the following balanced equation.

2 Fe³⁺(aq) + Sn²⁺(aq) ⇒ 2Fe²⁺(aq) + Sn⁴⁺(aq)

First, we have to calculate the moles of Sn²⁺ that react.

`(0.1015molSn^(2+) )/(1L) .13.28 * 10^(-3) L=1.348* 10^(-3)molSn^(2+)`

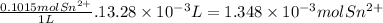
We also know the following relations:

• According to the balanced equation, 1 mole of Sn²⁺ reacts with 2 moles of Fe³⁺.
• 1 mole of Fe³⁺ is oxidized from 1 mole of Fe.
• The molar mass of Fe is 55.84 g/mol.

Then, for 1.348 × 10⁻3 moles of Sn²⁺:

`1.348* 10^(-3)molSn^(2+).(2molFe^(3+) )/(1molSn^(2+) ) .(1molFe)/(1molFe^(3+) ) .(55.84gFe)/(1molFe) =0.1505gFe`

If there are 0.1505 g of Fe in a 0.1875 g sample, the mass percentage of Fe is:

`(0.1505g)/(0.1875g) * 100 \% = 80.27\%`