Question

The radius of a circular puddle is growing at a rate of 25 cm/s.

(a) How fast is its area growing at the instant when the radius is 50 cm? HINT [See Example 1.] (Round your answer to the nearest integer.)


(b) How fast is the area growing at the instant when it equals 36 cm2? HINT [Use the area formula to determine the radius at that instant.] (Round your answer to the nearest integer.)

Answer 1

a) 2500π cm/s

b) 300√π cm/s

Explanation:

Given:

Rate of growth of radius,
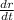`(dr)/(dt)` = 25 cm/s

Area of circle is given as:

A = πr²

a)Rate of growth of area,
`(dA)/(dt)=(d(\pi r^2))/(dt)`

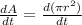
or

⇒
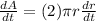`(dA)/(dt)=(2)\pi r(dr)/(dt)` ............(1)

at r = 50 cm

on substituting the respective values, we get

⇒
`(dA)/(dt)=(2)\pi r(dr)/(dt)`

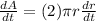
or

⇒
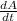`(dA)/(dt)` = 2π(50)25 = 2500π cm/s

b) when area , A = 36 cm²

36 = πr²

r =
`(6)/(√(\pi))`

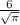
thus, using (1)

⇒
`(dA)/(dt)=(2)\pi r(dr)/(dt)`

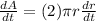
on substituting the respective values, we get

⇒
`(dA)/(dt)=(2)\pi ((6)/(√(\pi)))25`

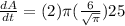
or

⇒
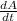`(dA)/(dt)` = 300√π cm/s